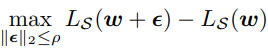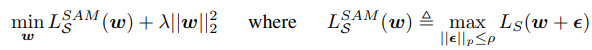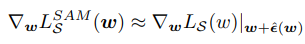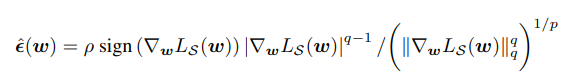기존에 자주 사용되던 RMSprop, ADAM 등과 달리 loss sharpness를 함께 고려하여 변수를 업데이트하는 방법인 SAM(Sharpness-Aware Minimization) optimizer를 사용해 ImageNet에서 SOTA를 달성한 논문. 기존에 사용되던 optimizer는 결국 loss를 낮추는 것만이 최종 목적이기 때문에 학습이 suboptimal하거나 overfitting에 취약하다는 문제점이 있었는데, SAM은 모델의 성능과 안정성을 더욱 높이기 위해 비교적 평평한 landscape에서 minimum을 찾는다고 이해할 수 있다. 이러한 설계는 기존 연구를 통해 밝혀진 loss shaprness와 모델의 generalization ability에 높은 상관관계가 있다는 사실에 기반한다. 아래의 그림을 보면, SGD를 사용한 경우(왼쪽)보다 SAM을 사용했을 때(오른쪽) 더 스무스한 local minimum으로 수렴하는 것을 확인할 수 있다.

사실 optimizer가 loss sharpness를 고려하도록 하는 설계는 이전부터 존재했는데, SAM이 이러한 기존 시도들과 다른 점은 알고리즘이 단순해서 scalability가 뛰어나, 거대한 모델에도 활용할 수 있다는 점이다. SAM에서는 loss sharpness term을 아래와 같이 정의한다.

의미를 해석하면, 현재 모델 변수들이 놓인 지점에서 반지름이 $ \rho $인 초구(차원은 업데이트하는 모델 변수의 수가 될 것이다) 안에 놓인 모든 점들에 대해 loss를 구했을 때, 가장 큰 값을 갖는 지점이 현재의 loss와 얼만큼의 차이를 보이는가를 묻는 것이다. 따라서, sharpness가 심할수록 주변 위치에서의 loss가 크게 변할 것이므로 아래의 term은 큰 값을 가지게 된다. SAM optimizer는 이를 바탕으로 다음과 같이 정의된 값을 minimize하게 된다. 현재 위치에 놓인 지점 뿐만 아니라 근처의 지점들도 모두 낮은 loss를 가져야만 낮은 값을 갖도록 설계되었음을 알 수 있다. 또한, L2 regularization term이 더해진 것을 볼 수 있다.

이제 남은 문제는 위와 같이 정의된 값의 gradient를 구하는 것인데, 테일러 전개를 통한 근사를 사용한다. 자세한 계산과정을 생략하면, 아래와 같이 gradient를 근사할 수 있다. 위의 식에 등장하는 $\hat\epsilon(w)$는 아래와 같이 구할 수 있다. 결론적으로, 우리는 두 번의 gradient 계산만으로 sharpness-aware minimization을 구현할 수 있게 된다. 이러한 단순한 연산이 SAM이 효율적이면서 높은 성능을 보일 수 있는 이유이다.

실험 결과, SAM을 사용해 학습했을 때에는 다른 모든 조건이 동일한 상태에서 SAM 대신 기존의 SGD를 사용해 학습한 경우보다 더욱 우수한 성능을 보여주었다. 또한, 저자는 SAM이 finetuning에 사용했을 때에도 높은 성능을 보이며, label noise에 대한 robustness 에서도 강점을 가진다는 것을 확인하였다. 이러한 장점들로 인해 앞으로 더욱 많은 연구에서 SAM optimizer를 사용할 것으로 기대된다.

논문 링크 및 이미지 출처: https://arxiv.org/abs/2010.01412